What influence does the choice of dice have? Quite a few people come up with the idea of replacing the two six-sided dice with one twelve-sided dice. It saves dice and possibly some time when rolling. But what influence does this have on the game mechanics of Battletech Alpha Strike?

Let’s remember the different methods for rolling dice in the combat phase. What they have in common is that a critical hit is also generated on a result of 12. In the case of critical hits, a 2 (ammunition chamber hit) and a 12 (fatal cockpit hit) are usually fatal for a target.
This means that if I choose a dice layout that increases the probability of a 2 or a 12, then I will tend to get more of these hits during the course of the game.
On the other hand, I have to achieve a certain dice result in order to hit. Can I increase my chances of hitting if I choose a twelve-sided dice layout? Let’s compare 2D6 (two six-sided dice) and 1w12 (one twelve-sided dice) using probability theory.
What does the probability theory say?
To understand the difference in probability between a twelve-sided dice (1w12) and the sum of two six-sided dice (2D6), we analyze the probability distributions of the possible outcomes.
1. Twelve-sided dice (1D12):
A d12 has the numbers from 1 to 12, and each number has an equal probability of around 8.33% (1/12). This is an even (uniform) distribution.
2. sum of two six-sided dice (2D6):
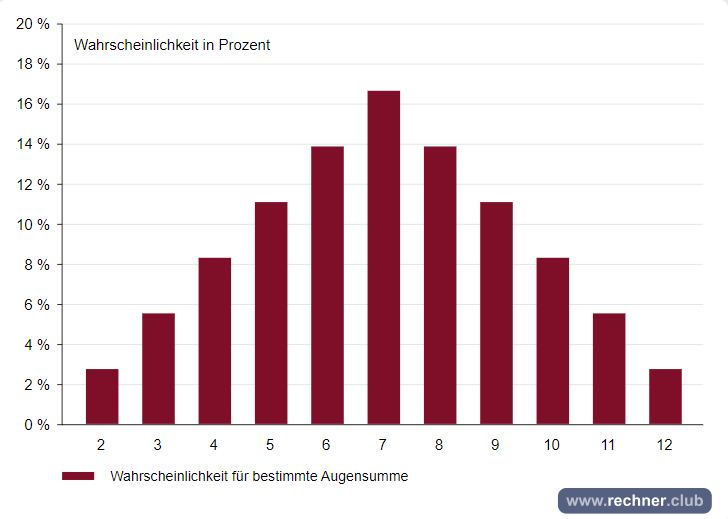
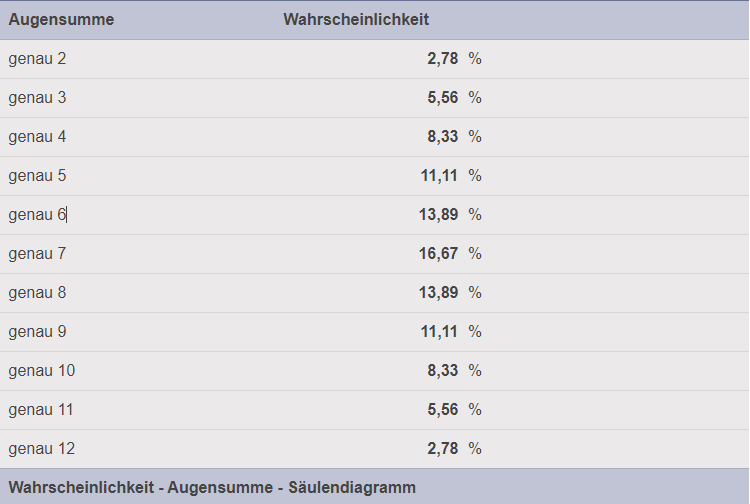
When rolling two d6 dice, the sum of the two dice is between 2 and 12. However, the probabilities are not equally distributed, as there are more opportunities to roll medium values (such as 7) than extreme values (such as 2 or 12). The distribution is triangular (with a peak in the middle).
- Number of combinations per result:
- Sum 2: 1 combination (1+1)(1+1)(1+1)
- Sum 3: 2 combinations (1+2,2+1)(1+2, 2+1)(1+2,2+1)
- Sum 4: 3 combinations (1+3,2+2,3+1)(1+3, 2+2, 3+1)(1+3,2+2,3+1)
- …
- Total 7: 6 combinations (1+6,2+5,3+4,4+3,5+2,6+1)(1+6, 2+5, 3+4, 4+3, 5+2, 6+1)(1+6,2+5,3+4,4+3,5+2,6+1)
- …
- Total 12: 1 combination (6+6)(6+6)(6+6)
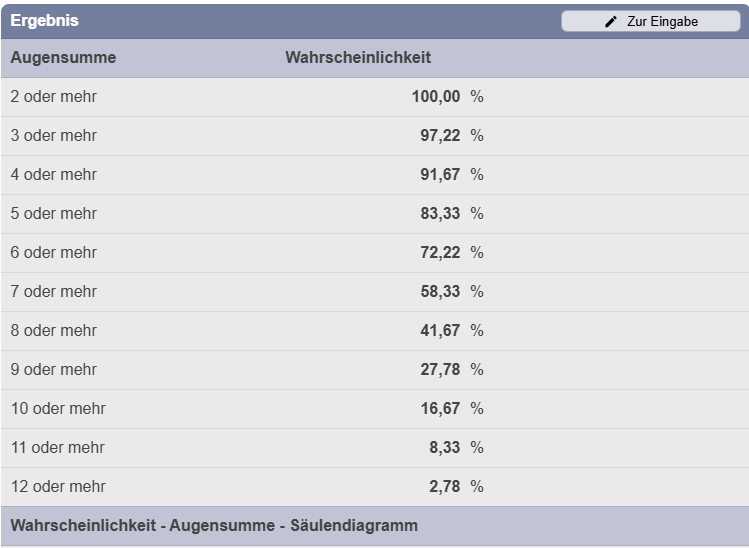
- Probabilities: The total number of possible combinations is 6×6=366 \times 6 = 366×6=36, as each of the 6 numbers on the first dice can be combined with each of the 6 numbers on the second dice. The probabilities for each sum result from the number of combinations divided by 36:
- Total 2: ≈2.78%
- Total 3: ≈5.56%
- Total 4: ≈8.33%
- …
- Sum 7: ≈16.67% (highest probability)
- …
- Total 12: 1≈2.78%
3. Comparison:
The probabilities of the two scenarios differ as follows:
- 1D12 (evenly distributed):
- Each number from 1 to 12 has a constant probability of ≈8.33%.
- 2w6 (triangular distribution):
- The probabilities are different and depend on the sum.
- Extreme values (2, 12) are the least likely ≈2.78%.
- Average values (e.g. 7) are most likely ≈16.67%.
The most important differences:
- With 1w12, every result is equally likely.
- With 2w6, medium values are clearly preferred, while extreme values are rarer.
4. graphical representation of the distribution for 2w6:
2D6: A bell curve (triangular) with a peak at 7.
Example:
- The probability of rolling a 7 on a d12 is 8.33%.
- The probability of getting the sum 7 with 2d6 is 16.67% – twice as high.
Summarizedsignificance for the game mechanics
- 1D12 offers a constant probability for all results.
- 2w6 prefers medium results and has a lower probability of extremes.
As a result, with a 1w12 it should happen more often that you hit at all. Even high dice values such as an 11 or 12 have a higher probability compared to the 2D6 method. But fatal critical hits are also more likely with a 1w12. This is because the probabilities for a 2 or 12 are significantly higher compared to the 2D6.
Which is better? I prefer the 2D6 method. But there’s nothing wrong with using 1w12 if you accept that (fatal) hits, or hits for which a high dice value is necessary (e.g. long range attacks), occur more frequently on average.



