Welcher Einfluss hat die Wahl des Würfels? Nicht wenige kommen auf die Idee die zwei sechsseitigen Würfel durch einen zwölfseitigen Würfel zu ersetzen. Spart man da doch Würfel und evt. etwas Zeit beim würfeln. Aber welchen Einfluss hat das auf die Spielmechanik von Battletech Alpha Strike?

Dazu erinnern wir uns mal die unterschiedlichen Methoden zum Auswürfeln in der Kampfphase. Denen gemein ist das bei einem Ergebnis von 12, auch ein kritischer Treffer erzeugt wird. Bei den kritischen Treffern ist eine 2 (Munitionskammer-Treffer) und eine 12 (tödlicher Cockpit-Treffer) für ein Ziel i.d.R. tödlich.
Das Bedeutet, das wenn ich eine Würfellayout wähle welches die Wahrscheinlichkeiten für eine 2 oder eine 12 erhöht, dann bekomme ich im Spielverlauf auch tendenziell mehr von diesen Treffern.
Auf der anderen Seite muss ich, um zu treffen, ein bestimmtes Würfelergebnis erzielen. Kann ich meine Chancen erhöhen zu treffen, wenn ich eine zwölfseitiges Würfellayout wähle? Vergleichen wir doch einfach mal 2w6 (zwei sechseitige Würfel) und 1w12 (ein zwölfseitiger Würfel) mit Hilfe der Wahrscheinlichkeitsrechnung.
Was sagt die Wahrscheinlichkeitsrechnung ?
Um den Wahrscheinlichkeitsunterschied zwischen einem zwölfseitigen Würfel (1w12) und der Summe zweier sechsseitiger Würfel (2w6) zu verstehen, analysieren wir die Wahrscheinlichkeitsverteilungen der möglichen Ergebnisse.
1. Zwölfseitiger Würfel (1w12):
Ein d12 hat die Zahlen von 1 bis 12, und jede Zahl hat eine gleiche Wahrscheinlichkeit von etwa 8,33 % (1/12). Es handelt sich um eine gleichmäßige (uniforme) Verteilung.
2. Summe zweier sechsseitiger Würfel (2w6):
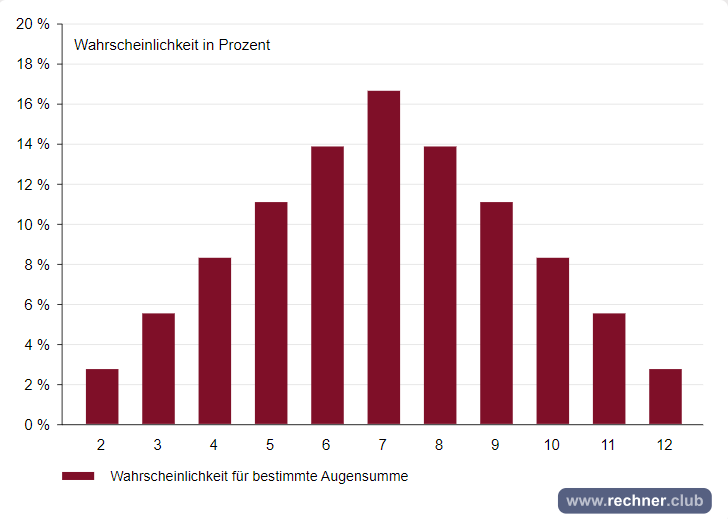
Beim Wurf von zwei d6-Würfeln liegt die Summe der beiden Würfel zwischen 2 und 12. Allerdings sind die Wahrscheinlichkeiten nicht gleich verteilt, da es mehr Möglichkeiten gibt, mittlere Werte zu würfeln (wie 7) als extreme Werte (wie 2 oder 12). Die Verteilung ist triangular (mit einer Spitze in der Mitte).
- Anzahl der Kombinationen pro Ergebnis:
- Summe 2: 1 Kombination (1+1)(1+1)(1+1)
- Summe 3: 2 Kombinationen (1+2,2+1)(1+2, 2+1)(1+2,2+1)
- Summe 4: 3 Kombinationen (1+3,2+2,3+1)(1+3, 2+2, 3+1)(1+3,2+2,3+1)
- …
- Summe 7: 6 Kombinationen (1+6,2+5,3+4,4+3,5+2,6+1)(1+6, 2+5, 3+4, 4+3, 5+2, 6+1)(1+6,2+5,3+4,4+3,5+2,6+1)
- …
- Summe 12: 1 Kombination (6+6)(6+6)(6+6)
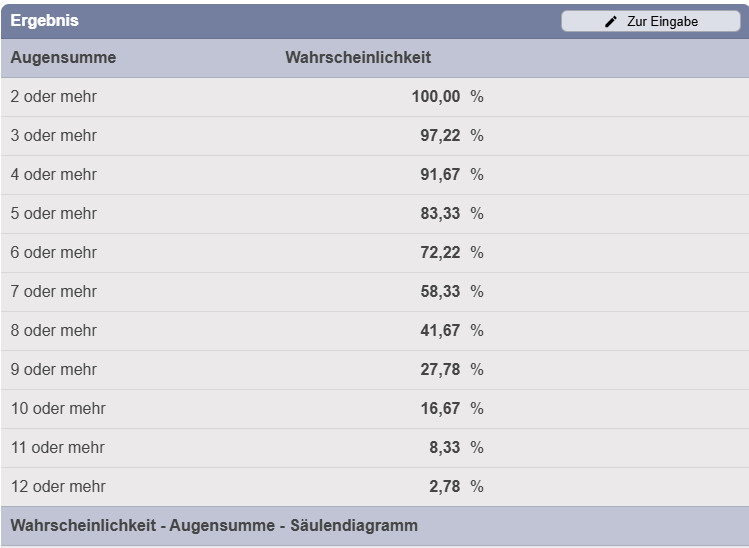
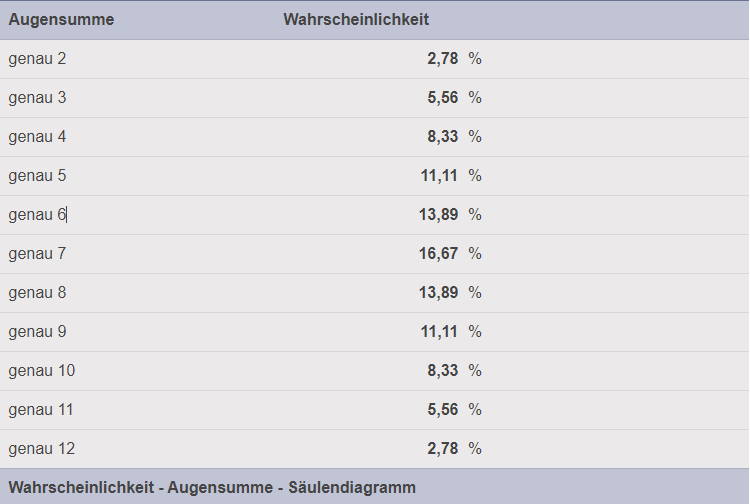
- Wahrscheinlichkeiten: Die Gesamtzahl möglicher Kombinationen ist 6×6=366 \times 6 = 366×6=36, da jede der 6 Zahlen des ersten Würfels mit jeder der 6 Zahlen des zweiten Würfels kombiniert werden kann. Die Wahrscheinlichkeiten für jede Summe ergeben sich aus der Anzahl der Kombinationen, geteilt durch 36:
- Summe 2: ≈2,78%
- Summe 3: ≈5,56%
- Summe 4: ≈8,33%
- …
- Summe 7: ≈16,67% (höchste Wahrscheinlichkeit)
- …
- Summe 12: 1≈2,78%
3. Vergleich:
Die Wahrscheinlichkeiten der beiden Szenarien unterscheiden sich wie folgt:
- 1w12 (gleichmäßig verteilt):
- Jede Zahl von 1 bis 12 hat eine konstante Wahrscheinlichkeit von ≈8,33%.
- 2w6 (triangular verteilt):
- Die Wahrscheinlichkeiten sind unterschiedlich und hängen von der Summe ab.
- Extreme Werte (2, 12) sind am unwahrscheinlichsten ≈2,78%.
- Mittlere Werte (z. B. 7) sind am wahrscheinlichsten ≈16,67%.
Die wichtigsten Unterschiede:
- Beim 1w12 ist jedes Ergebnis gleich wahrscheinlich.
- Bei 2w6 werden mittlere Werte deutlich bevorzugt, während extreme Werte seltener sind.
4. Grafische Darstellung der Verteilung bei 2w6:
2d6: Eine Glockenkurve (triangular) mit einer Spitze bei 7.
Beispiel:
- Die Wahrscheinlichkeit, bei einem d12 eine 7 zu würfeln, beträgt 8,33 %.
- Die Wahrscheinlichkeit, bei 2d6 die Summe 7 zu erhalten, ist 16,67 % – also doppelt so hoch.
Zusammenfassende Bedeutung für die Spielmechanik
- 1w12 bietet eine konstante Wahrscheinlichkeit für alle Ergebnisse.
- 2w6 bevorzugt mittlere Ergebnisse und hat eine geringere Wahrscheinlichkeit für Extreme.
Daraus resultiert das mit einem 1w12 es häufiger vorkommen sollte, das man überhaupt trifft. Denn auch hohe Würfelwerte wie eine 11 oder 12 haben gegenüber der 2w6 Methode höhere Wahrscheinlichkeiten. Aber auch fatale kritische Treffer sind mit einem 1w12 eher möglich. Denn die Wahrscheinlichkeiten für eine 2 bzw. 12 sind gegenüber dem 2w6 deutlich höher.
Was ist nun besser? Mir ist die 2w6 Methode lieber. Aber es spricht auch nichts dagegen 1w12 zu nehmen, wenn man akzeptiert das (fatale) Treffer, bzw. Treffer für di eein hoher Würfelwert notwendig ist (z.B: long range Angriffe) dadurch im Schnitt häufiger vorkommen.



